Untwerp fanfotonyskyntegreare sirkwy
Fotonyske yntegreare circuits(PIC) wurde faak ûntwurpen mei help fan wiskundige skripts fanwegen it belang fan paadlingte yn interferometers of oare tapassingen dy't gefoelich binne foar paadlingte.PICwurdt makke troch meardere lagen (meastal 10 oant 30) op in wafer te patterjen, dy't gearstald binne út in protte polygonale foarmen, faak fertsjintwurdige yn it GDSII-formaat. Foardat it bestân nei de fotomaskerfabrikant ferstjoerd wurdt, is it sterk winsklik om de PIC te simulearjen om de korrektheid fan it ûntwerp te ferifiearjen. De simulaasje is ferdield yn meardere nivo's: it leechste nivo is de trijediminsjonale elektromagnetyske (EM) simulaasje, wêrby't de simulaasje útfierd wurdt op it subgolflingtenivo, hoewol de ynteraksjes tusken atomen yn it materiaal op makroskopyske skaal behannele wurde. Typyske metoaden omfetsje trijediminsjonale eindige-ferskil tiiddomein (3D FDTD) en eigenmodusútwreiding (EME). Dizze metoaden binne it meast krekt, mar binne net praktysk foar de heule PIC-simulaasjetiid. It folgjende nivo is 2.5-diminsjonale EM-simulaasje, lykas eindige-ferskil strielpropagaasje (FD-BPM). Dizze metoaden binne folle rapper, mar offerje wat krektens op en kinne allinich paraksiale propagaasje behannelje en kinne bygelyks net brûkt wurde om resonators te simulearjen. It folgjende nivo is 2D EM-simulaasje, lykas 2D FDTD en 2D BPM. Dizze binne ek rapper, mar hawwe beheinde funksjonaliteit, lykas se gjin polarisaasjerotators simulearje kinne. In fierder nivo is transmissie- en/of ferspriedingsmatrikssimulaasje. Elke haadkomponint wurdt werombrocht ta in komponint mei ynfier en útfier, en de ferbûne golflieder wurdt werombrocht ta in fazeferskowings- en ferswakkingselemint. Dizze simulaasjes binne ekstreem rap. It útfiersignaal wurdt krigen troch de transmissiematriks te fermannichfâldigjen mei it ynfiersignaal. De ferspriedingsmatriks (waans eleminten S-parameters neamd wurde) fermannichfâldiget de ynfier- en útfiersignalen oan 'e iene kant om de ynfier- en útfiersignalen oan 'e oare kant fan 'e komponint te finen. Yn prinsipe befettet de ferspriedingsmatriks de refleksje yn it elemint. De ferspriedingsmatriks is meastal twa kear sa grut as de transmissiematriks yn elke diminsje. Gearfetsjend presintearret elke laach fan simulaasje in ôfwaging tusken snelheid en krektens, en ûntwerpers kieze it juste nivo fan simulaasje foar har spesifike behoeften om it ûntwerpfalidaasjeproses te optimalisearjen.
It fertrouwen op elektromagnetyske simulaasje fan bepaalde eleminten en it brûken fan in ferspriedings-/oerdrachtmatrix om de heule PIC te simulearjen garandearret lykwols gjin folslein korrekt ûntwerp foar de streamplaat. Bygelyks, ferkeard berekkene paadlengten, multimode-golflieders dy't net effektyf hege-oarder modi ûnderdrukke, of twa golflieders dy't te ticht byinoar binne en liede ta ûnferwachte koppelingsproblemen, sille wierskynlik net ûntdutsen wurde tidens simulaasje. Dêrom, hoewol avansearre simulaasje-ark krêftige ûntwerpfalidaasjemooglikheden leverje, fereasket it noch altyd in hege mjitte fan waakzaamheid en soarchfâldige ynspeksje troch de ûntwerper, kombineare mei praktyske ûnderfining en technyske kennis, om de krektens en betrouberens fan it ûntwerp te garandearjen en it risiko fan it streamskema te ferminderjen.
In technyk mei de namme sparse FDTD makket it mooglik om 3D- en 2D FDTD-simulaasjes direkt op in folslein PIC-ûntwerp út te fieren om it ûntwerp te falidearjen. Hoewol it foar elk elektromagnetysk simulaasje-ark lestich is om in PIC op tige grutte skaal te simulearjen, is de sparse FDTD yn steat om in frij grut lokaal gebiet te simulearjen. Yn tradisjonele 3D FDTD begjint de simulaasje mei it ynisjalisearjen fan 'e seis komponinten fan it elektromagnetyske fjild binnen in spesifyk kwantisearre folume. Mei de tiid wurdt de nije fjildkomponint yn it folume berekkene, ensafuorthinne. Elke stap fereasket in soad berekkening, dus it duorret lang. Yn sparse 3D FDTD wurdt, ynstee fan by elke stap op elk punt fan it folume te berekkenjen, in list mei fjildkomponinten byhâlden dy't teoretysk oerienkomme kinne mei in willekeurich grut folume en allinich foar dy komponinten berekkene wurde. By elke tiidstap wurde punten neist fjildkomponinten tafoege, wylst fjildkomponinten ûnder in bepaalde krêftdrompel weilitten wurde. Foar guon struktueren kin dizze berekkening ferskate oarders fan grutte rapper wêze as tradisjonele 3D FDTD. Sparse FDTDS prestearje lykwols net goed by it omgean mei dispersive struktueren, om't dit tiidfjild te folle ferspriedt, wat resulteart yn listen dy't te lang en lestich te behearjen binne. Figuer 1 lit in foarbyldskermôfbylding sjen fan in 3D FDTD-simulaasje fergelykber mei in polarisaasjebeamsplitter (PBS).
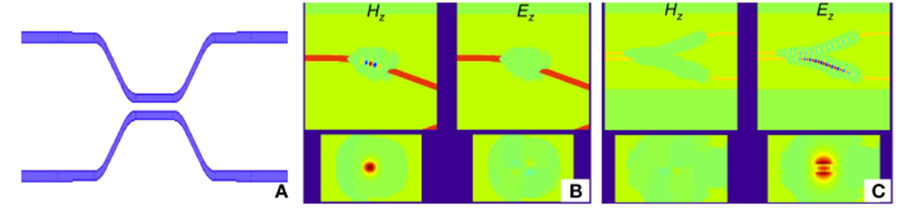
Figuer 1: Simulaasjeresultaten fan 3D sparse FDTD. (A) is in boppe-oansicht fan 'e struktuer dy't simulearre wurdt, dat is in rjochtingskoppeling. (B) Toant in skermôfbylding fan in simulaasje mei quasi-TE-eksitaasje. De twa diagrammen hjirboppe litte it boppe-oansicht sjen fan 'e quasi-TE- en quasi-TM-sinjalen, en de twa diagrammen hjirûnder litte de oerienkommende dwerssnit sjen. (C) Toant in skermôfbylding fan in simulaasje mei quasi-TM-eksitaasje.
Pleatsingstiid: 23 july 2024





